Sondipon Adhikari

Professor Sondipon Adhikari (FRAeS)
Professor of Engineering Mechanics
James Watt School of Engineering
The University of Glasgow
Glasgow G12 8QQ, United Kingdom
Phone: + 44 (0) 141 330 2032
Email: Sondipon.Adhikari@glasgow.ac.uk, Sondipon.Adhikari@gmail.com
Twitter Linkedin

 
 
 
 
 
Uncertainty Quantification in Computational Mechanics
A word-cloud from the title of the journal papers
Figure: A word-cloud from the title of the journal papers

Professor Adhikari's research works in this field contribute to the following sub areas: Computational methods are used extensively for the analysis and design of engineering dynamic systems such as automobiles, aircrafts and wind-turbines. Credible computational methods can lessen the need for expensive experimental analysis and prototype building and reduce the cost of development of these products. Some engineers believe that the credibility of computational predictions can be enhanced only by using intensive numerical approaches, e.g., by increasing the mesh density in the finite element model of a structure. While this may be necessary for some applications (e.g., modelling the tip of a crack) it is not sufficient to improve the credibility of computational prediction. This is due to the fact that several types of uncertainties exist in the whole process of science-based computational predictions as shown in the figure below. Such uncertainties include (a) parametric uncertainty (e.g, uncertainty in geometric parameters, friction coefficient, viscosity, strength of the materials involved), and (b) nonparametric uncertainty such as those arising from model inadequacy (e.g., using linear law when it is actually nonlinear) and low fidelity models (e.g., damping, multi-scale issues, damage mechanisms). These uncertainties must be assessed and managed for reliable computational predictions.
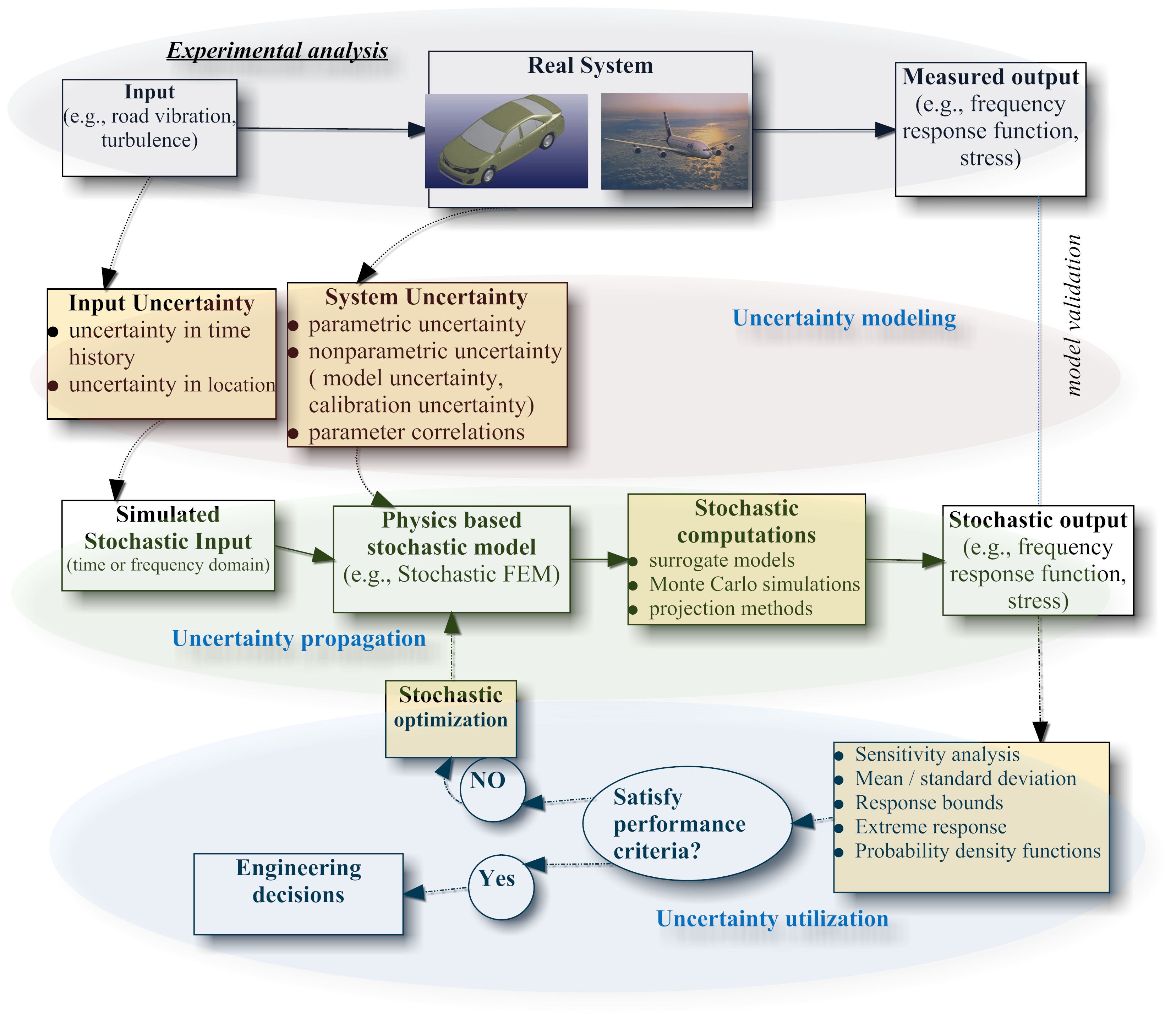Uncertainty in computational science
Figure: The role of uncertainty in computational analysis and design of engineering systems (FEM: Finite Element Method)

Based on what information is available, several types of problems arise in computational structural mechanics:

Input System Output Problem name Main techniques
Known (deterministic) Known (deterministic) Unknown Analysis (forward problem) FEM/BEM/Finite difference
Known (deterministic) Incorrect (deterministic) Known (deterministic) Updating/calibration Modal updating
Known (deterministic) Unknown Known (deterministic) System identification Kalman filter
Assumed (deterministic) Unknown (deterministic) Prescribed Design Design optimisation
Known Partially Known Known Structural Health Monitoring (SHM) SHM methods
Known (deterministic) Known (deterministic) Prescribed Control Modal control
Known (random) Known (deterministic) Unknown Random vibration Random vibration methods
Known (deterministic) Known (random) Unknown Uncertainty propagation (forward problem) SFEM/SEA/RMT
Known (random/deterministic) Known (random) Known from experiment and model (random) Model validation Validation methods
Known (random/deterministic) Known (random) Known from different computations (random) Model verification verification methods
Known (random) Incorrect (random) Known (random) Probabilistic updating/calibration Bayesian calibration
Assumed (random/deterministic) Unknown (random) Prescribed (random) Probabilistic design RBOD
Known (random/deterministic) Partially known (random) Partially known (random) Joint state and parameter estimation Particle Kalman Filter/Ensemble Kalman Filter
Table: Different types of problems arising in computational structural mechanics (RBOD: Reliability Based Optimal Design; SEEA: Statistical Energy Analysis; RMT: Random Matrix Theory)

Specific research interests include:

  • Novel projection approaches for the Stochastic Finite Element Analysis (SFEA)
  • Random Matrix Theory (RMT)
  • Random eigenvalue problems arising in random matrices and stochastic differential operators
  • Solution of stochastic partial differential equations and stochastic algebraic equations
  • Experimental methods
  • Gaussian Process (GP) emulators
  • Surrogate modelling methods for complex stochastic systems
  • Fuzzy uncertainty propagation
A brief description of the research topics and some key journal publications are given below.

C.1. Dynamics of stochastic systems

Multiple degrees of freedom dynamic systems with random parameters are considered. The computational paradigm for structural dynamic systems with uncertainties can be sketched in terms of (1) the deterministic dimension (N: degrees of freedom (DOF) of the FE model), (2) the stochastic dimension (M: number of random variables), and (c) the time dimension (t: the length of time for the dynamic simulation). As shown in the figure, existing computational methods work well for smaller stochastic and time dimensions only (e.g., 10-20 oscillation cycles and up to 20 random variables for a 1M DOF problem). This poses a serious bottleneck in delivering probabilistic designs for industrial scale problems. Our experience shows that surrogate model-based methods, normally used for such problems, may work well for static problems but can be difficult to apply for dynamic problems (see the picture below).
Our unique vision on this is to use physics-based surrogate models as opposed to complete data-based surrogates (such as the so-called polynomial chaos). For dynamic problems, this will include the use of vibration modes and frequencies. This way, not only engineers can relate uncertainty quantification to their existing knowledge, but also can use existing finite element software for computation. The broad aim of this research is to produce a step-change in the performance analysis and design of dynamic structures by creating a paradigm that fully embraces uncertainty from the outset. This is crucially needed to overcome the predominant practice whereby designs are restricted to a deterministic regime despite rapidly increasing demands to consider unavoidable uncertainties from technological, economic and safety considerations. The ambition is to go beyond the conventional safety-factor based design, to unravel the huge potential, which can be gained by exploiting the explicit consideration of uncertainty. Our aspiration is to obtain novel stochastic modelling and simulation techniques, which will enable the most efficient design and manufacture of the next-generation dynamic structures.

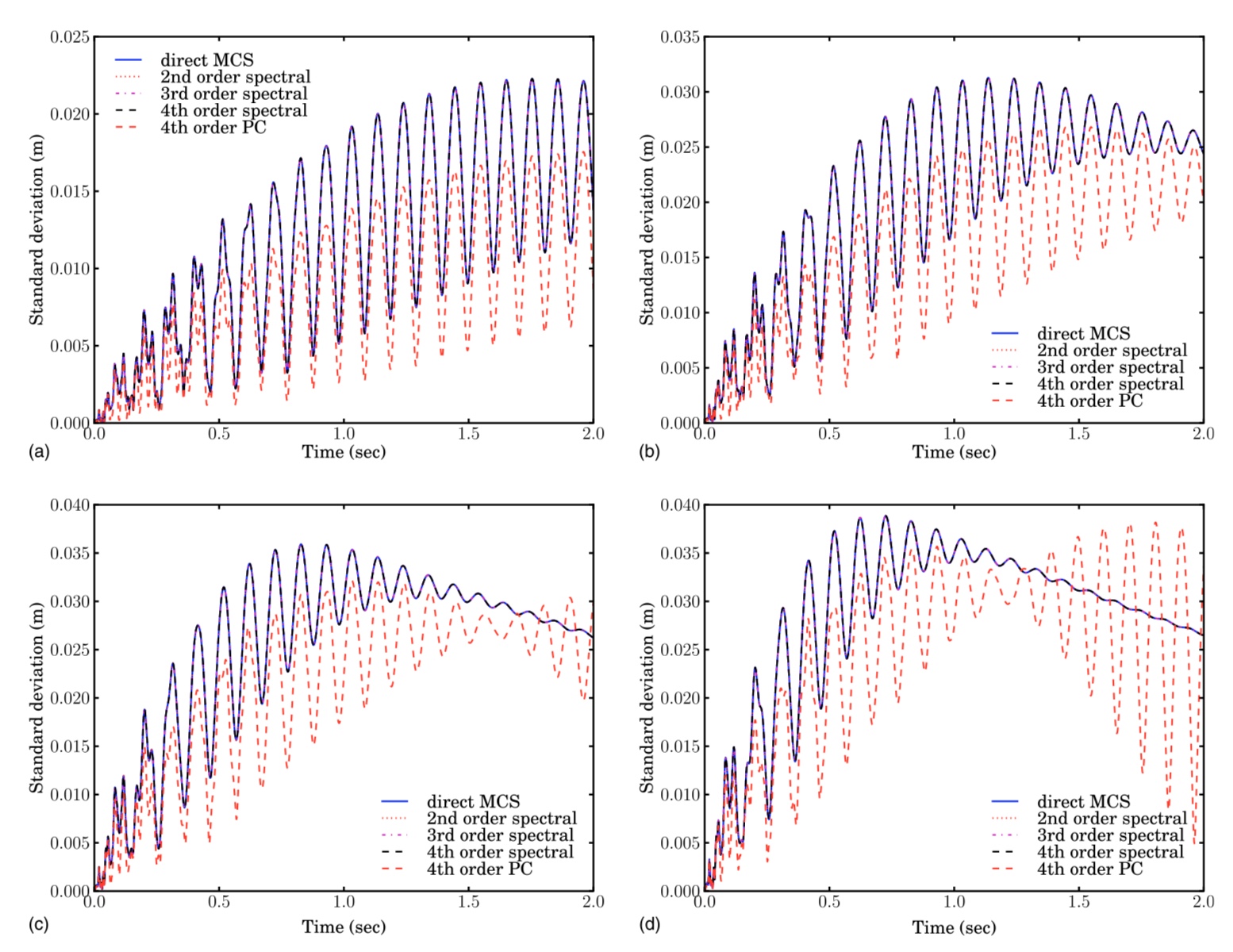
Standard deviation of the deflection of the free end of a cantilever beam
Figure: Standard deviation of the deflection of the free end of a cantilever beam under unit impulse load

Key Journal Publications

  1. Jacquelin, E., Brizard, D., Adhikari, S., and Friswel, M. I., “Time-domain response of damped stochastic multiple-degree-of-freedom systems,” ASCE Journal of Engineering Mechanics, in press.
  2. Dey, S., Mukhopadhyay, T., Naskar, S., Dey, T. K., Chalak, H. D., and Adhikari, S., “Probabilistic characterization for dynamics and stability of laminated soft core sandwich plates,” Journal of Sandwich Structures and Materials, Vol. 21, No. 1, 2019, pp. 366-397.
  3. Pryse, S. E., Adhikari, S., and Kundu, A., “Sample-based and sample-aggregated Galerkin projection schemes for structural dynamics,” Probabilistic Engineering Mechanics, Vol. 338, No. 8, 2018, pp. 412-439.
  4. Dey, S., Mukhopadhyay, T., Sahu, S. K., and Adhikari, S., “Stochastic dynamic stability analysis of composite curved panels subjected to non-uniform partial edge loading,” European Journal of Mechanics - A/Solids, Vol. 67, No. 1-2, 2018, pp. 108-122.
  5. Jacquelin, E., Dessombz, O., Sinou, J.-J., Adhikari, S., and Friswel, M. I., “Polynomial chaos based eXtended Pade expansion in structural dynamics,” International Journal for Numerical Methods in Engineering, Vol. 111, No. 12, 2017, pp. 1170-1191.
  6. Dey, S., Mukhopadhyay, T., Adhikari, S., Spickenheuer, A., and Gohs, U., “Uncertainty quantification in natural frequency of composite plates - An Artificial neural network based approach,” Advanced Composite Letter, Vol. 25, No. 2, 2016, pp. 43-48.
  7. Dey, S., Mukhopadhyay, T., Sahu, S. K., and Adhikari, S., “Probabilistic characterization for dynamics and stability of laminated soft core sandwich plates,” Journal of Sandwich Structures and Materials, 2018, in press.
  8. Mukhopadhyay, T., Chakraborty, S., Dey, S., Adhikari, S., and Chowdhury, R., “A critical assessment of Kriging model variants for high-fidelity uncertainty quantification in dynamics of composite shells,” Archives of Computational Methods in Engineering,Vol. 24, No. 3, 2017, pp. 495-518.
  9. Jacquelin, E., Adhikari, S., Sinou, J.-J., and Friswell, M. I., “The role of roots of orthogonal polynomials in the dynamic response of stochastic systems,” ASCE Journal of Engineering Mechanics, Vol. 142, No. 8, 2015, pp. 06016004:1-8.
  10. Dey, S., Mukhopadhyay, T., Sahu, S. K., and Adhikari, S., “Effect of cutout on stochastic natural frequency of composite curved panels,” Composites Part B, Vol. 105, No. 11, 2016, pp. 188-202.
  11. Dey, S., Mukhopadhyay, T., Spickenheuer, A., Adhikari, S., and Heinrich, G., “Bottom up surrogate based approach for stochastic frequency response analysis of laminated composite plates,” Composite Structures, Vol. 140, No. 4, 2016, pp. 712-727.
  12. Jacquelin, E., Friswel, M. I., Adhikari, S., Dessombz, O., and Sinou, J.-J., “Polynomial chaos expansion with random and fuzzy variables,” Mechanical Systems and Signal Processing, Vol. 75, No. 6, 2016, pp. 41-56.
  13. Mukhopadhyay, T., Dey, S., and Adhikari, S., “On quantifying the effect of noise in surrogate based stochastic free vibration analysis of composite laminates,” Composite Structures, Vol. 140, No. 4, 2016, pp. 798-805.
  14. Kundu, A., Adhikari, S., and Friswell, M. I., “Transient response analysis of randomly parametrized finite element systems based on approximate balanced reduction,” Computer Methods in Applied Mechanics and Engineering, Vol. 285, No. 3, 2015, pp. 542-570.
  15. Dey, S., Mukhopadhyay, T., and Adhikari, S., “Stochastic free vibration analyses of composite doubly curved shells - A Kriging model approach,” Composites Part B: Engineering, Vol. 70, No. 3, 2015, pp. 99-112.
  16. Adhikari, S. and Pascual, B., “The ‘damping effect’ in the dynamic response of stochastic oscillators,” Probabilistic Engineering Mechanics, Vol. 44, No. 4, 2016, pp. 2-17.
  17. Jacquelin, E., Adhikari, S., Sinou, J.-J., and Friswell, M. I., “Polynomial chaos expansion and steady-state response of a class of random dynamical systems,” ASCE Journal of Engineering Mechanics, Vol. 106, No. 6, 2015, pp. 061901:1-4.
  18. Kundu, A. and Adhikari, S., “Dynamic analysis of stochastic structural systems using frequency adaptive spectral functions,” Probabilistic Engineering Mechanics, Vol. 39, No. 1, 2015, pp. 23-38.
  19. Kundu, A. and Adhikari, S., “Transient response of structural dynamic systems with parametric uncertainty,” ASCE Journal of Engineering Mechanics, Vol. 140, No. 2, 2014, pp. 315-331.
  20. DiazDelaO, F. A., Kundu, A., Adhikari, S., and Friswell, M. I., “Hybridization of spectral function approach with Bayesian emulators for stochastic structural dynamics,” Computer Methods in Applied Mechanics and Engineering, Vol. 270, No. 3, 2014, pp. 201-209.
  21. DiazDelaO, F. A., Adhikari, S., Flores, E. I. S., and Friswell, M. I., “Stochastic structural dynamic analysis using Gaussian process emulators,” Computers and Structures,Vol. 120, No. 1, 2013, pp. 24-32.
  22. Pascual, B. and Adhikari, S., “Combined parametric-nonparametric uncertainty quantification using random matrix theory and polynomial chaos expansion,” Computers a and Structures, Vol. 112-113, No. 12, 2012, pp. 84-94.
  23. Adhikari, S., “Doubly spectral stochastic finite element method (DSSFEM) for structural dynamics,” ASCE Journal of Aerospace Engineering, Vol. 24, No. 3, 2011, pp. 264-276.
  24. Adhikari, S. and Friswell, M. I., “Shaped modal sensors for linear stochastic beams,” Journal of Intelligent Material Systems and Structures, Vol. 20, No. 18, December 2009, pp. 2269-2284.
  25. Adhikari, S. and Manohar, C. S., “Transient dynamics of stochastically parametered beams,” ASCE Journal of Engineering Mechanics, Vol. 126, No. 11, November 2000, pp. 1131-1140.
  26. Adhikari, S. and Manohar, C. S., “Dynamic analysis of framed structures with statistical uncertainties,” International Journal for Numerical Methods in Engineering,Vol. 44, No. 8, 1999, pp. 1157-1178.
  27. Manohar, C. S. and Adhikari, S., “Dynamic stiffness of randomly parametered beams,” Probabilistic Engineering Mechanics, Vol. 13, No. 1, January 1998, pp. 39-51.
  28. Manohar, C. S. and Adhikari, S., “Statistical analysis of vibration energy flow in randomly parametered trusses,” Journal of Sound and Vibration, Vol. 217, No. 1, 1998, pp. 43-74.

C.2. Random eigenvalue problem

Random eigenvalue problems arise in the dynamic analysis of linear stochastic systems - for example in the problem of dynamic response prediction of cars rolling out from a production chain, cabin noise prediction of nominally identical helicopters across the fleet and vibrations across the ensemble of MEMS (Micro Electro Mechanical Systems) divides. The study of probabilistic characterisation of the eigensolutions of random matrix and differential operators is now an important research topic in the field of stochastic structural mechanics. The aim of studying random eigenvalue problems is to obtain the joint probability density function of the eigenvalues and the eigenvectors. The current literature on random eigenvalue problems arising in engineering systems is dominated by the mean-centred perturbation methods. We develop novel methods based on asymptotic analysis and metamodels.
Vibration modes of a MWCNT Mean and standard deviation of fundamental natural frequency 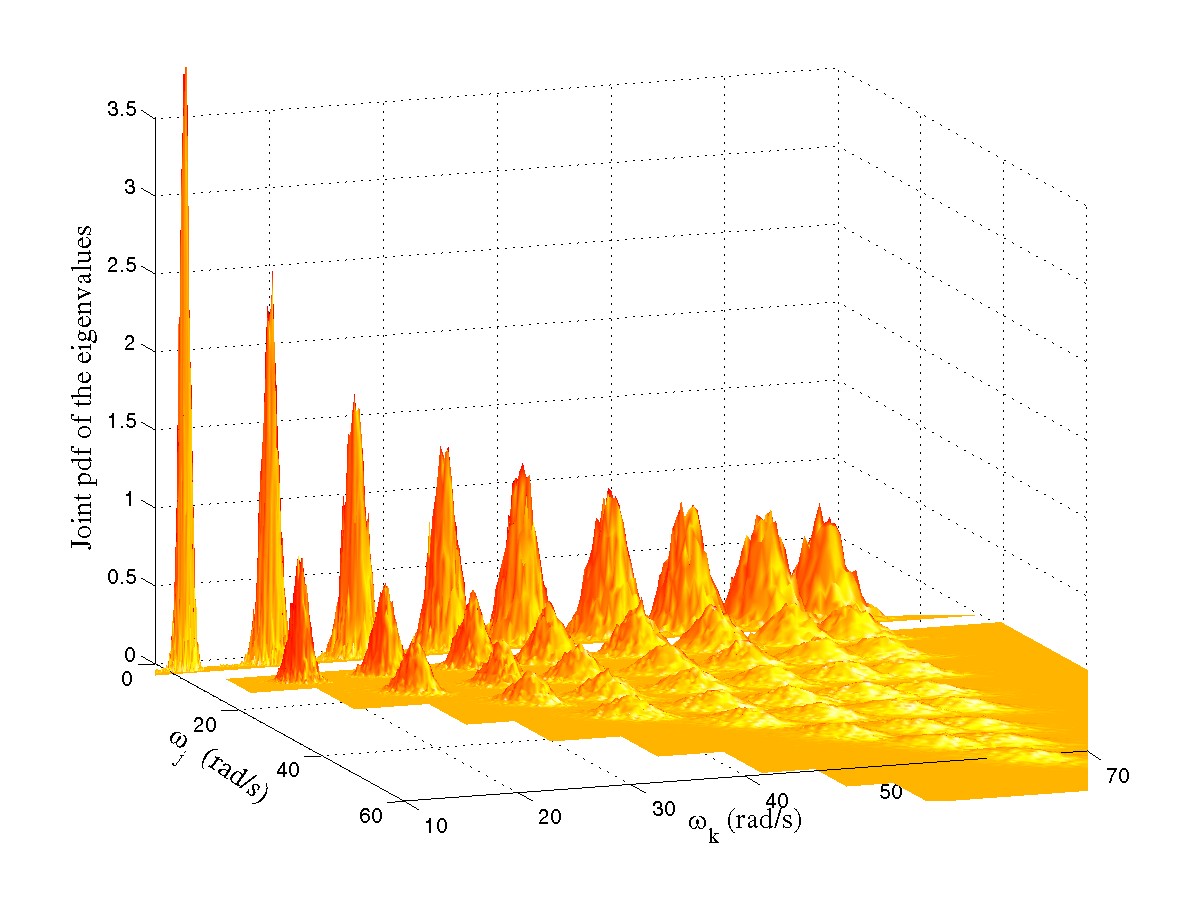Joint natural frequency statistics Joint natural frequency statistics

Key Journal Publications

  1. Pryse, S. E. and Adhikari, S., “Stochastic finite element response analysis using random eigenfunction expansion,” Computers and Structures, Vol. 192, No. 11, 2017, pp. 1-15.
  2. Naskar, S., Mukhopadhyay, T., Sriramula, S., and Adhikari, S., “Stochastic natural frequency analysis of damaged thin-walled laminated composite beams with uncertainty in micromechanical properties,” Composites Part B, Vol. 160, No. 1, 2017, pp. 312-334.
  3. Dey, S., Naskar, S., Mukhopadhyay, T., Gohs, U., Spickenheuer, A., Bittrich, L., Sriramula, S., Adhikari, S., and Heinrich, G., “Uncertain natural frequency analysis of composite plates including effect of noise - A polynomial neural network approach,” Composite Structures, Vol. 143, No. 5, 2016, pp. 130-142.
  4. Dey, S., Mukhopadhyay, T., Adhikari, S., and Khodaparast, H. H., “Stochastic natural frequency of composite conical shells,” Acta Mechanica, Vol. 226, No. 8, 2015, pp. 2537-2553.
  5. Dey, S., Mukhopadhyay, T., and Adhikari, S., “Stochastic free vibration analysis of angle-ply composite plates - A RS-HDMR approach,” Composite Structures, Vol. 122, No. 4, 2015, pp. 526-536.
  6. Pascual, B. and Adhikari, S., “Hybrid perturbation-polynomial chaos approaches to the random algebraic eigenvalue problem,” Computer Methods in Applied Mechanics and Engineering, Vol. 217-220, No. 1, 2012, pp. 153-167.
  7. Adhikari, S., Pastur, L., Lytova, A., and Du-Bois, J. L., “Eigenvalue-density of linear stochastic dynamical systems: A random matrix approach,” Journal of Sound and Vibration, Vol. 331, No. 5, 2012, pp. 1042-1058.
  8. Adhikari, S. and Phani, A. S., “Random eigenvalue problems in structural dynamics: Experimental investigations,” AIAA Journal, Vol. 48, No. 6, 2010, pp. 1085-1097.
  9. Adhikari, S., “Joint statistics of natural frequencies of stochastic dynamic systems,” Computational Mechanics, Vol. 40, No. 4, September 2007, pp. 739-752.
  10. Adhikari, S. and Friswell, M. I., “Random matrix eigenvalue problems in structural dynamics,” International Journal for Numerical Methods in Engineering, Vol. 69, No. 3, 2007, pp. 562-591.
  11. Adhikari, S., “Random eigenvalue problems revisited,” Sadhana- Proceedings of the Indian Academy of Engineering Sciences, Vol. 31, No. 4, August 2006, pp. 293-314 (Special Issue on Probabilistic Structural Dynamics and Earthquake Engineering).
  12. Wagenknecht, T., Green, K., Adhikari, S., and Michiels, W., “Structured pseudospectra and random eigenvalues problems in vibrating systems,” AIAA Journal, Vol. 44, No. 10, October 2006, pp. 2404-2414.
  13. Adhikari, S., “Complex modes in stochastic systems,” Advances in Vibration Engineering, Vol. 3, No. 1, 2004, pp. 1-11.

C.3. Random matrix theory for structural dynamics

A random matrix can be considered as an observable phenomenon representable in the form of a matrix which under repeated observation yields different non-deterministic outcomes. Therefore, a random matrix is simply a collection of random variables which may satisfy certain rules (for example symmetry, positive definiteness etc). Random matrices were introduced by Wishart (1928) in the context of multivariate statistics. However, the Random Matrix Theory (RMT) was not used in other branches until the 1950s when Wigner published his works (leading to the Nobel prize in Physics in 1963) on the eigenvalues of random matrices arising in high-energy physics. Using an asymptotic theory for large dimensional matrices, Wigner was able to bypass the Schrodinger equation and explain the statistics of measured atomic energy levels in terms of the limiting eigenvalues of these random matrices. Since then research on random matrices has continued to attract interests in multivariate statistics, physics, number theory and more recently in mechanical and electrical engineering. We use Wishart random matrices to directly model mass, damping and stiffness matrices as they are positive definite matrices. Random matrix model has also been validated against experimental results.
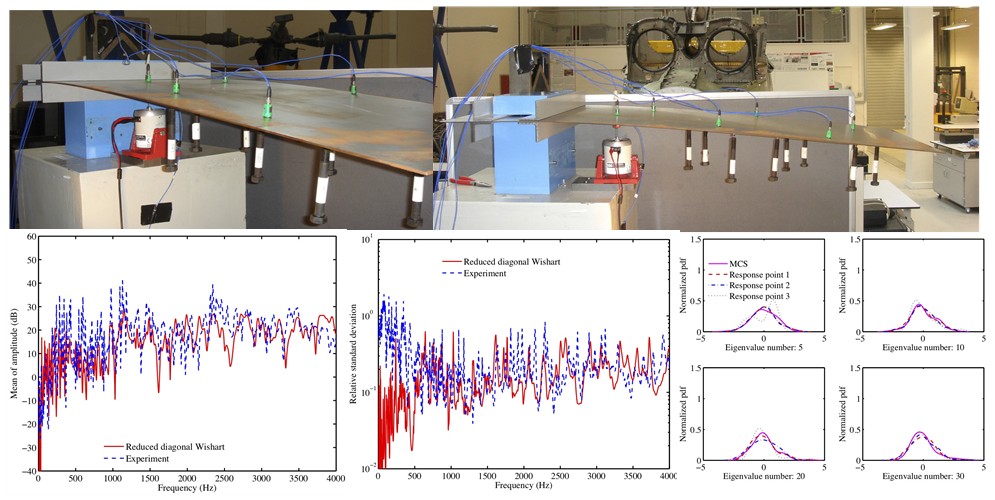Wishart random matrix model Figure: Experimental comparison of the results from Wishart random matrix model

Key Journal Publications

  1. Jacquelin, E., Adhikari, S., Sinou, J.-J., and Friswell, M. I., “Polynomial chaos expansion in structural dynamics: Accelerating the convergence of the first two statistical moment sequences,” Journal of Sound and Vibration, Vol. 356, No. 11, 2015, pp. 144-154.
  2. Dey, S., Mukhopadhyay, T., Sahu, S. K., Li, G., , Rabitz, H., and Adhikari, S., “Thermal uncertainty quantification in frequency responses of laminated composite plates,” Composite Part B, Vol. 80, No. 6, 2015, pp. 186-197.
  3. Dey, S., Mukhopadhyay, T., Adhikari, S., Khodaparast, H. H., and Kerfriden, P., “Rotational and ply-level uncertainty in response of composite conical shells,” Composite Structures, Vol. 131, No. 6, 2015, pp. 594-605.
  4. Adhikari, S., “Uncertainty quantification in structural dynamics using non-central Wishart distribution,” International Journal of Engineering Under Uncertainty: Hazards, Assessment and Mitigation, Vol. 2, No. 3-4, 2010, pp. 123-139.
  5. Adhikari, S. and Chowdhury, R., “A reduced-order non-intrusive approach for stochastic structural dynamics,” Computers and Structures, Vol. 88, No. 21-22, 2010, pp. 1230-1238.
  6. Adhikari, S., “Generalized Wishart distribution for probabilistic structural dynamics,” Computational Mechanics, Vol. 45, No. 5, May 2010, pp. 495-511.
  7. Adhikari, S. and Sarkar, A., “Uncertainty in structural dynamics: experimental validation of wishart random matrix model,” Journal of Sound and Vibration, Vol. 323, No. 3-5, 2009, pp. 802-825.
  8. Adhikari, S., Friswell, M. I., Lonkar, K., and Sarkar, A., “Experimental case studies for uncertainty quantification in structural dynamics,” Probabilistic Engineering Mechanics,Vol. 24, No. 4, October 2009, pp. 473-492.
  9. Adhikari, S., “Wishart random matrices in probabilistic structural mechanics,” ASCE Journal of Engineering Mechanics, Vol. 134, No. 12, December 2008, pp. 1029-1044.
  10. Adhikari, S., “On the quantification of damping model uncertainty,” Journal of Sound and Vibration, Vol. 305, No. 1-2, September 2007, pp. 153-171.
  11. Adhikari, S., “Matrix variate distributions for probabilistic structural mechanics,” AIAA Journal, Vol. 45, No. 7, July 2007, pp. 1748-1762.

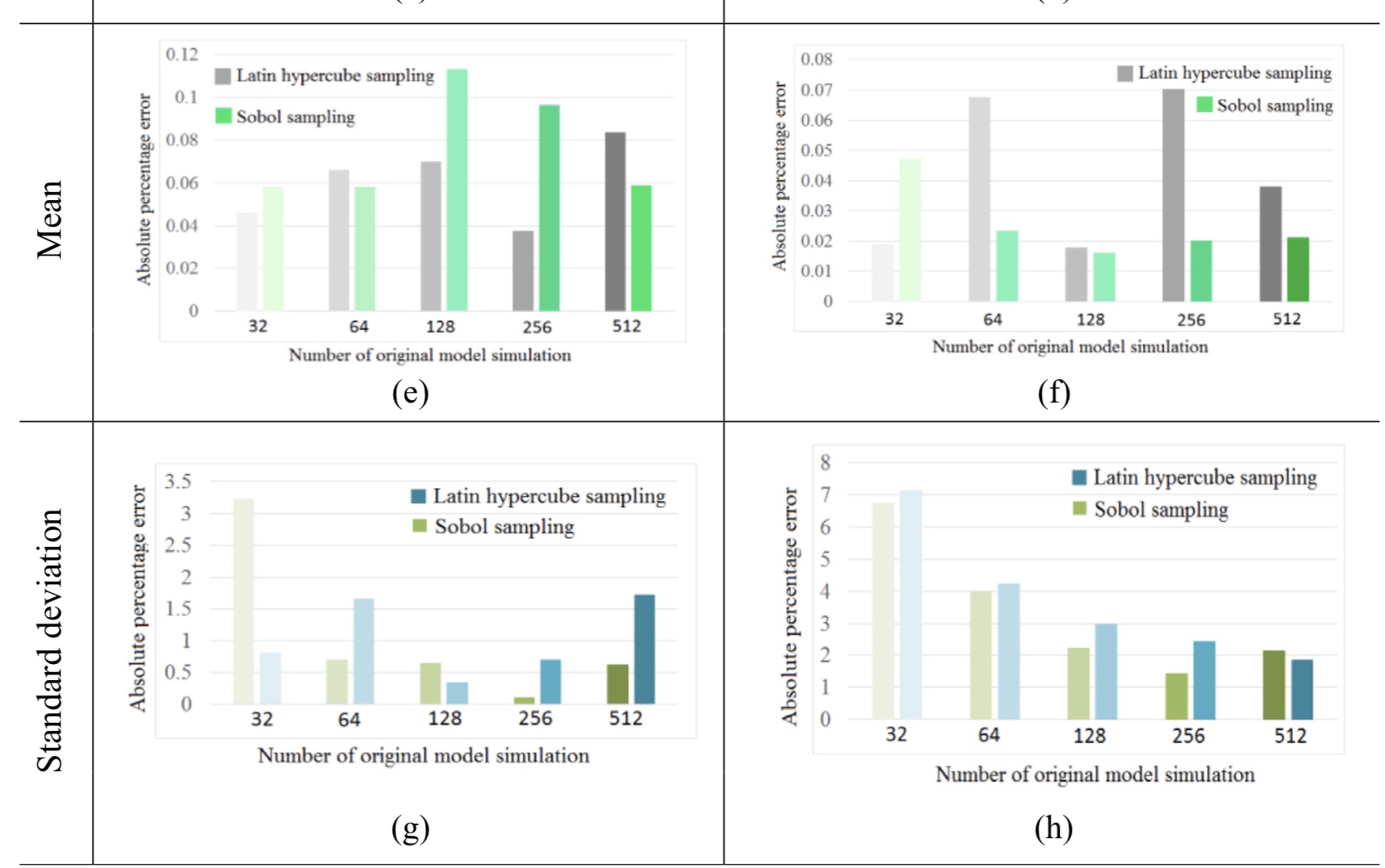
C.4. Computational methods for uncertainty propagation

Realistic prediction of response of engineering structures with uncertainties is necessary to predict and monitor the health of a structure. Traditionally uncertainties have been accounted for in an ad-hoc way through the use of safety factors. Such an approach is unlikely to be satisfactory to meet ambitious design targets in the future. For example, one of the main goals set in Flightpath 2050 'Streamlined systems engineering, design, manufacturing, certification and upgrade processes have addressed complexity and significantly decreased development costs (including a 50% reduction in the cost of certification'. The situation may also arise when system safety is being jeopardised due to the lack of detailed treatment of uncertainty, for example, the finite probability of a resonance occurring is unlikely to be captured by a safety-factor based approach due to the intricate nonlinear relationships between the system parameters and the natural frequencies.
Over the past four decades, several approaches have been developed to explicitly account uncertainties in structural dynamics. These broadly divide into two branches: (a) when the forcing is random, and (b) when the system is random. For the first branch, since the late 60s, random vibration methods have been developed. This is now a mature research field, rich with useful results which are now routinely used in practice. Examples include building and bridges subjected to an uncertain earthquake or wind loads, offshore platforms subjected to random wave loads.
The techniques in the second branch are being developed and can be divided according to the nature of the uncertainties they address, namely, (i) parametric methods and (ii) non-parametric methods. The state-of-the-art parametric approach is the stochastic finite element method. Over the past three decades, significant developments have taken place in stochastic finite element analysis. These can be broadly divided into (1) simulation-based methods (e.g., Monte Carlo Simulation, Importance sampling), and (2) analytical and semi-analytical methods (e.g., perturbation methods, polynomial chaos (PC) method). Simulation-based approaches are accurate but computationally expensive. PC technique, on the other hand, becomes computationally expensive if a large number of variables are involved. Consequently, many authors have proposed reduced-order methods and surrogate models to improve computational efficiency. Our research belongs to this class of approaches.
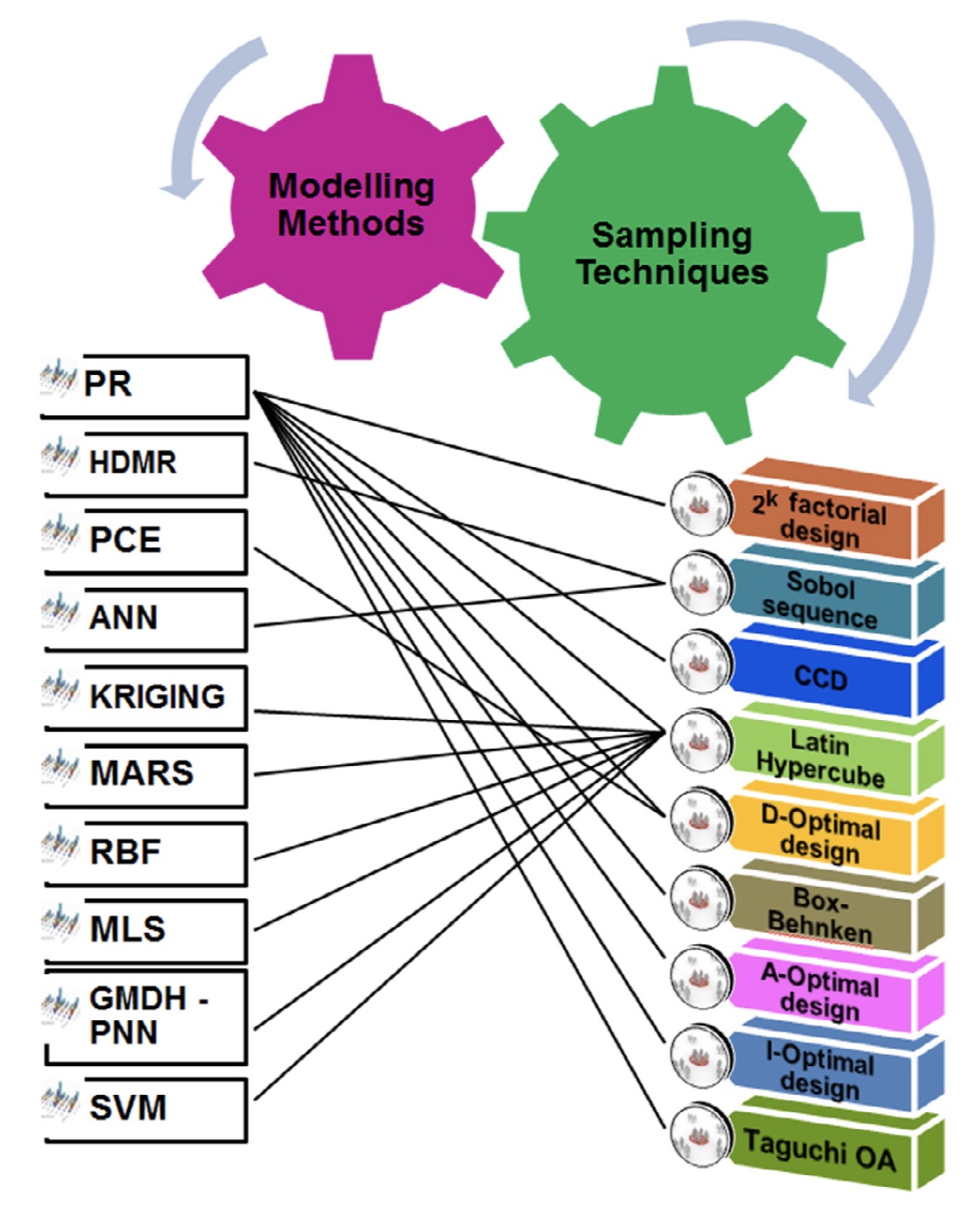Surrogate modelling methods The mapping of surrogate modelling methods and corresponding sampling techniques 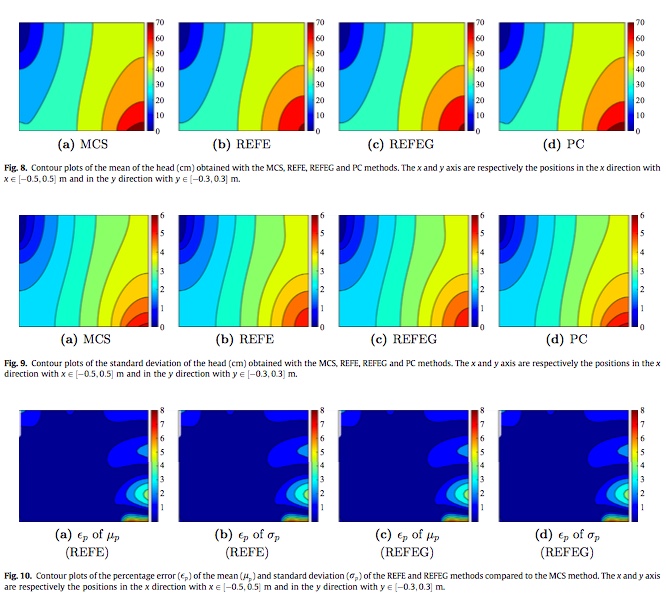Reduced order stochastic computational model Error arising from the use of a reduced-order stochastic computational model

Key Journal Publications

  1. Scarth, C., Cabral, S. A. P. H., Silva, G. H. C., and Prado, A. P., “Random field simulation over curved surfaces: Applications to computational structural mechanics,” AIAA Journal, Vol. 345, No. 3, 2019, pp. 283-301.
  2. Scarth, C. and Adhikari, S., “Modelling spatially varying uncertainty in composite structures using lamination parameters,” AIAA Journal, Vol. 55, No. 11, 2017, pp. 3951-3965.
  3. Chakraborty, S., Chatterjee, T., Chowdhury, R., and Adhikari, S., “A surrogate based multi-fidelity approach for robust design optimization,” Applied Mathematical Modelling,Vol. 47, No. 7, 2017, pp. 726-744.
  4. Dey, S., Mukhopadhyay, T., and Adhikari, S., “Metamodel based high-fidelity stochastic analysis of composite laminates: A concise review with critical comparative assessment,” Composite Structures, Vol. 171, No. 7, 2017, pp. 227-250.
  5. Pryse, S. E. and Adhikari, S., “Eigenfunction expansion based Galerkin approaches for stochastic finite element analysis,” Meccanica dei Materiali e delle Strutture, Vol. 6, No. 1, 2017, pp. 74-81.
  6. Metya, S., Mukhopadhyay, T., Adhikari, S., and Bhattacharya, G., “System reliability analysis of soil slopes with general slip surfaces using multivariate adaptive regression splines,” Computers and Geotechnics, Vol. 87, No. 7, 2017, pp. 212-228.
  7. Mukhopadhyay, T., Mahata, T., Dey, S., and Adhikari, S., “Probabilistic analysis and design of HCP nano-wires: An efficient surrogate based molecular dynamics simulation approach,” Journal of Materials Science & Technology, Vol. 32, No. 12, 2016, pp. 1345-1351.
  8. Garcia-Macias, E., Castro-Triguero, R., Friswell, M. I., Adhikari, S., and Saez, A., “Metamodel-based approach for stochastic free vibration analysis of functionally graded carbon nanotube reinforced plates,” Composite Structures, Vol. 152, No. 9, 2016, pp. 183-198.
  9. Mahata, A., Mukhopadhyay, T., and Adhikari, S., “A polynomial chaos expansion based molecular dynamics study for probabilistic strength analysis of nano-twinned copper,” Materials Research Express, Vol. 3, No. 3, 2016, pp. 036501:1-13.
  10. Dey, S., Mukhopadhyay, T., Khodaparast, H. H., and Adhikari, S., “Fuzzy uncertainty propagation in composites using Gram-Schmidt polynomial chaos expansion,” Applied Mathematical Modelling, Vol. 40, No. 7-8, 2016, pp. 4412-4428.
  11. Potrykus, A. and Adhikari, S., “Response statistics of linear oscillators driven by time inhomogeneous Markov processes,” Development and Applications of Oceanic Engineering, 2018, in press.
  12. Kundu, A., Adhikari, S., and Friswell, M. I., “Stochastic finite elements of discretely parametrized random systems on domains with boundary uncertainty,” International Journal for Numerical Methods in Engineering, Vol. 100, No. 3, 2014, pp. 183-221.
  13. Adhikari, S. and Khodaparast, H. H., “A spectral approach for fuzzy uncertainty propagation in finite element analysis,” Fuzzy Sets and Systems, Vol. 243, No. 1, 2014, pp. 1-24.
  14. Chowdhury, R. and Adhikari, S., “Fuzzy parametric uncertainty analysis of linear dynamical systems: A surrogate modeling approach,” Mechanical System and Signal Processing, Vol. 32, No. 10, 2012, pp. 5-17.
  15. Pascual, B. and Adhikari, S., “A reduced polynomial chaos approach for stochastic finite element analysis,” S a dhan a - Proceedings of the Indian Academy of Engineering Sciences, Vol. 37, No. 3, 2012, pp. 319-340.
  16. Murugan, S., Chowdhury, R., Adhikari, S., and Friswell, M. I., “Helicopter aeroelastic analysis with spatially uncertain rotor blade properties,” Aerospace Science and Technology, Vol. 16, No. 1, 2012, pp. 29-39.
  17. DiazDelaO, F. A. and Adhikari, S., “Bayesian assimilation of multi-fidelity finite element models,” Computers and Structures, Vol. 92-93, No. 2, 2012, pp. 206-215.
  18. Chowdhury, R. and Adhikari, S., “Reliability analysis of uncertain dynamical systems using correlated function expansion,” International Journal of Mechanical Sciences,Vol. 53, No. 4, 2011, pp. 281-285.
  19. DiazDelaO, F. A. and Adhikari, S., “Gaussian process emulators for the stochastic finite element method,” International Journal of Numerical Methods in Engineering,Vol. 87, No. 6, 2011, pp. 521-540.
  20. Adhikari, S., “A reduced spectral function approach for the stochastic finite element analysis,” Computer Methods in Applied Mechanics and Engineering, Vol. 200, No. 21-22, 2011, pp. 1804-1821.
  21. Adhikari, S., Chowdhury, R., and Friswell, M. I., “High dimensional model representation method for fuzzy structural dynamics,” Journal of Sound and Vibration,Vol. 330, No. 7, 2011, pp. 1516-1529.
  22. Li, C. F., Adhikari, S., Cen, S., Feng, Y. T., and Owen, D. R. J., “A joint diagonalisation approach for linear stochastic systems,” Computers and Structures,Vol. 88, No. 19-20, 2010, pp. 1137-1148.
  23. Chowdhury, R. and Adhikari, S., “High-dimensional model representation for stochastic finite element analysis,” Applied Mathematical Modelling, Vol. 34, No. 12, 2010, pp. 3917-3932.
  24. Adhikari, S., “Sensitivity based reduced approaches for structural reliability analysis,” Sadhana - Proceedings of the Indian Academy of Engineering Sciences, Vol. 35, No. 3, 2010, pp. 319-339.
  25. Chowdhury, R. and Adhikari, S., “Stochastic sensitivity analysis using preconditioning approach,” Engineering Computations, Vol. 27, No. 7, 2010, pp. 841-862.
  26. Potrykus, A. and Adhikari, S., “Dynamical response of damped structural systems driven by jump processes,” Probabilistic Engineering Mechanics, Vol. 25, No. 3, 2010, pp. 305-314.
  27. Adhikari, S., “Asymptotic distribution method for structural reliability analysis in high dimensions,” Proceedings of the Royal Society of London, Series- A, Vol. 461, No. 2062, 2005, pp. 3141-3158.
  28. Adhikari, S., “Reliability analysis using parabolic failure surface approximation,” ASCE Journal of Engineering Mechanics, Vol. 130, No. 12, 2004, pp. 1407-1427.

Home | Research | Publications | Teaching | Lectures | Students and Post-docs | Education & awards | Professional activities | Contact | Departmental web page | Downloads
This page was by Sondipon Adhikari